Temporal Higher-Order TDA

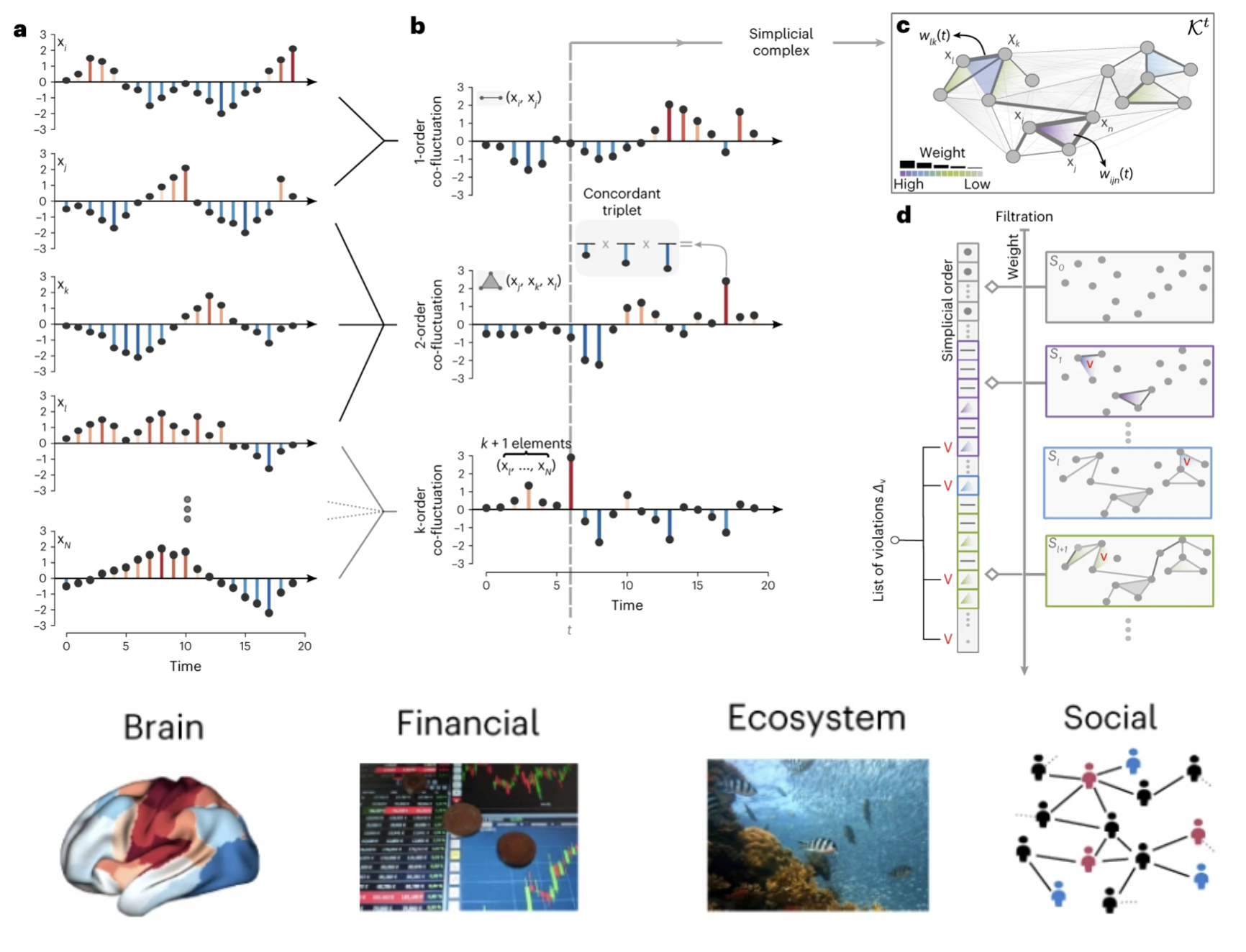
Background

Many real-world systems—financial markets, brain networks, ecosystems—are shaped by group interactions that evolve over time. Standard network tools focus on pairwise links and can miss these higher-order interactions (HOIs). Topological Data Analysis (TDA), via simplicial complexes and related operators, provides a principled way to model HOIs. This project develops a scalable, spectral approach to detect and analyze instantaneous k-way co-fluctuations in multivariate temporal data.

Project Description

This project is both computational and theoretical. The student will be involved in refining and implementing a recent framework to analyze multivariate time-series. Key tasks will include: 1) Understanding the mathematics of spectral theory and TDA for temporal data; 2) Implementing the method to detect "k-order co-fluctuations" from signals; 3) Validating the approach by testing it on synthetic signals to assess its performance and scalability. 4) Applying the new method to a real-world dataset (e.g., social or financial data) to uncover novel insights.

Requirements

• Strong background in linear algebra; familiarity with graph theory and signal processing.
• Good knowledge of a programming language (e.g. Python, Julia, Matlab); .
• Interest in numerical methods, TDA, and complex systems; willingness to learn new theory as needed.
• Ability to work with abstract concepts.