Reducibility of Multivariate Signals

Background

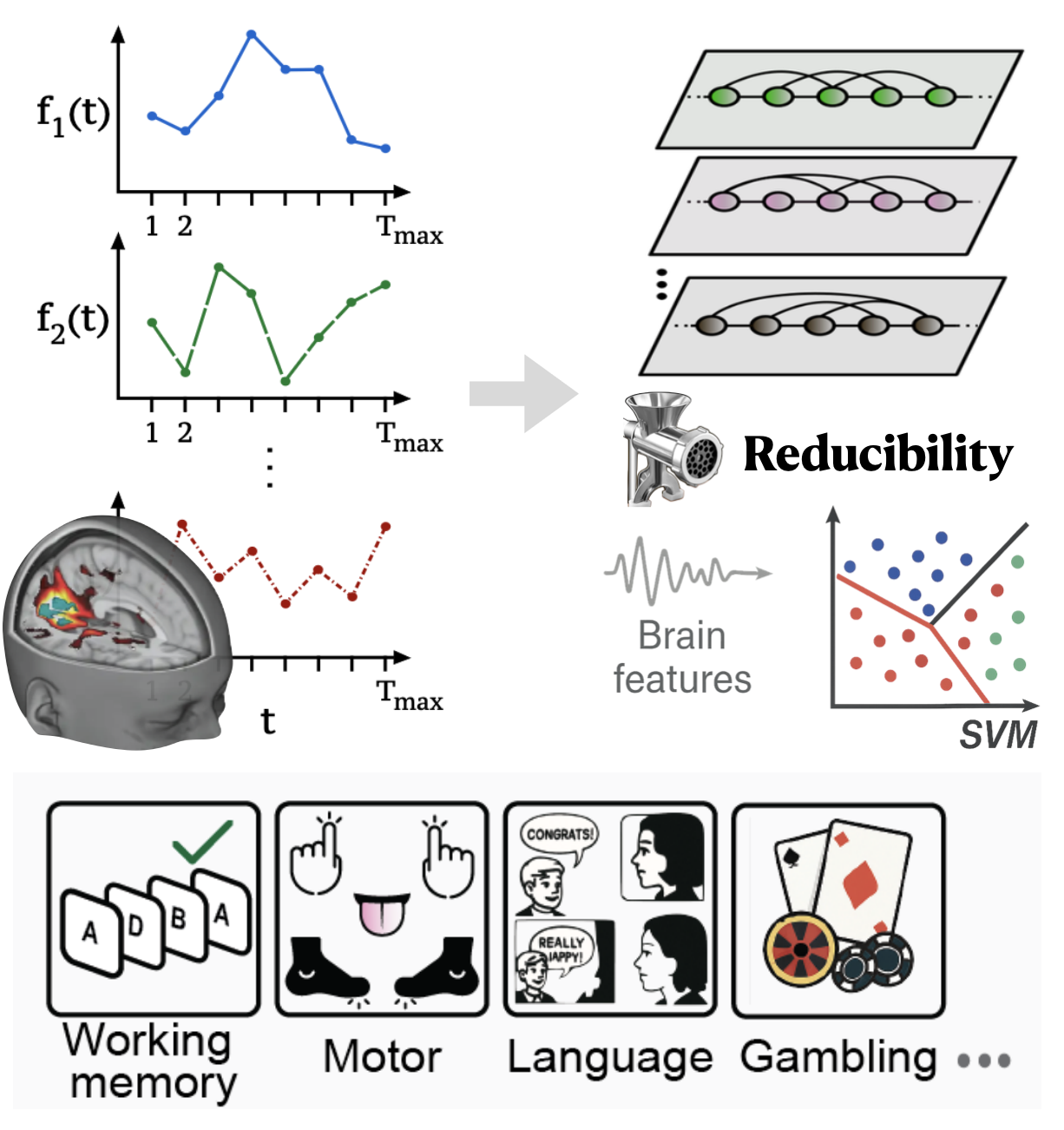
Complex systems, such as the human brain, are often measured using hundreds of simultaneous time-series (multivariate signals). It is a significant challenge to determine how much of this information is unique and how much is redundant. Understanding if these high-dimensional signals can be "reduced" to a simpler, more fundamental representation is key for both modeling and classification. This project will explore a novel multiplex approach, in which individual signals are mapped into graphs, to quantify the reducibility of temporal signals.

Project description

This project focuses on data analysis and method development. The student will: 1) Implement computational methods to transform multivariate time-series (e.g., f1(t), f2(t), ...) into a multiplex (multi-layer) network representation. 2) Develop and apply new metrics based on pairwise distance matrices and structural aggregation to quantify the reducibility of these signals. 3) Test the framework on various synthetic and real-world signals to characterize signals of different natures. 4) Investigate how these reduced signals can be leveraged for improved classification tasks.

Requirements

• Good programming skills (Python preferred).
• Background in, or motivation to learn, time-series analysis and network science.
• Interest in data reduction, machine learning, and complex systems.